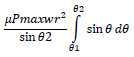Brakes: Design your own Disk Brakes - Part7

We all know drum brakes are an important part of life and learning to design them is extremely important but with the time of upgrading brakes into disc brakes, it is even more important that one must know the design aspects of disk brakes. In this article we will show how you can design your own disk brake and all the calculations and equations involved.

The above image represents a simple disc brakes and to understand the equations, one must understand the image above and now key to defining elements:

F = Force applied by the slave cylinder on the brake shoe

r = radius from center of disk to center of the brake pad

r_o = radius from center to outer surface of the brake pad

r_i = radius from center to inner radius of the brake pad

θ₁ = angle from horizontal to heel of brake pad

θ₂ = angle from horizontal to toe of brake pad
P_max = maximum applied pressure (depends on frictional material)
P = Uniformly distributed pressure along brake pad
Now, one more things to take into account is, in disc brakes there are 2 conditions that persists! 1) Uniform Pressure: which is applicable for new brakes & 2) Uniform Wear: which comes after a certain amount of use. Now, Work done is directly proportional to P_max X r_i therefore, W = k.P_max.r_i and since W & k are constants, let, W/k = K = P_max.r_i, Also, K = P.r, therefore,
P = P_max.r_i/r
Now, the force applied on the brake pads (F) is equal to

F = 

Replacing P with equation above and doing integration for θ, we get;

F = 

Again, doing integration for radius r, we get;

F = 

The equation above gives the force, now for torque;

τ = 

Replacing P with Pmax equation and integrating for θ, we get;

τ = 

Again, integrating for radius r, we get;

τ = 

Thus, the above equation gives torque for the disc brakes for uniform wear system!

Now to get equivalent radius (r_e) = τ/µF 

All the above equations hold good for Uniform wear system when work done is dependent on radius but when the brakes are new, then P = P_max because of which the new equations becomes;

F = 

Integrating for θ and solving for P, we get;

F = 

Thus, the final equations comes out to be;

F = 

Also for Torque (τ), the equations changes as;

τ = 

Integrating for θ and solving for P, we get;

τ = 

Thus, the final equation on integration of r comes out to be;

τ = 

With, this all the design equations have been discussed for the disc brakes, again, we know Torque = Force X Perpendicular length

Therefore, The Force applied by the force to stop the car will be F_brake = τ / r_e

Using this, we can solve any linear motion problem and calculate stopping distance and find time to decelerate the vehicle from velocity v to 0 using equations of motion.

Brakes: Design your own Drum Brakes - Part6

Well, we are nearly at the end of series with few more articles to go! Till date, we have already discussed nearly everything about construction, advantages, disadvantages and uses of each braking system but we, The Unicorn, understands that just understanding is not enough for anyone that is why we also make you understand how you can design the system yourself! As our motto says, Educate, Excel and then Innovate! To innovate you need to learn everything including how to design the system and the equations involved. In this article we will discuss the design aspects and equations involved in designing drum brakes.

To understand the design aspects of drum brakes, we have to understand the image above! First of all, as assumed we will say that direction of rotation of wheel is clockwise. Now the key to defining elements:

F = Force applied by the actuating device on each of the brake shoes.

P_max = Maximum Pressure applied

c = total displacement of heel and toe of the brake shoe

a = displacement from center of drum to the center axis of the brake shoe

r = radius of the drum from center of drum

b = displacement from center axis to the pivot point

Θ₁ = angle from center of pivot point to heel of shoe lining

Θ₂ = angle from center of pivot point to toe of shoe lining
Θ = average angle to distribute forces along the whole length of the shoe
and let µ = frictional coefficient of the shoe lining material

Since, the rotation is clockwise, the right shoe lining will attack first and its effect will be more than the trailing left shoe! and to calculate the force applied, we need to calculate the moment of inertia applied due to frictional force and also due to normal force acting on the shoe lining.
let's take k = P_max/SinΘ₂ therefore, k = P/sinΘ
equating both, we get; P = P_maxsinΘ/sinΘ₂ (where P is Uniformly distributed Pressure)
Now, Let M_f be the Moment of Inertia due to Frictional Force then,

M_f = 

Replacing P, we get:

M_f = 

Therefore, final formula after integration comes out to be:

M_f = 

Now, for calculating Moment of Inertia for Normal Force,

M_n = 

Replacing P in above equation,

M_n = 

After integration, final formula comes out to be:

M_n = 

Therefore, F = (M_f - M_n)/c

Also, Torque applied by the right shoe will be equal to

τr = 

replacing P, we get:

τr = 

The final equation becomes:

τr = 

Also, we need to add the force due to Left Shoe also called the trailing shoe;

For trailing shoe P'max = FcPmax/(Mf + Mn)

The torque applied by the left shoe will be:

τl = 

replacing P', the above equation becomes:

τl = 

The final equation becomes:

τl = 

The total Torque τ = τr + τl

Also, we know Torque = Force X Perpendicular length

Therefore, The Force applied by the force to stop the car will be F_brake = τ / Radius of Drum

Using this, we can solve any linear motion problem and calculate stopping distance and find time to decelerate the vehicle from velocity v to 0 using equations of motion.